初中九年级数学知识点总结：二次函数最简解析式 【y=ax平方】 的图象和性质

初中九年级数学知识点总结：二次函数最简解析式 【\(\displaystyle y=a{{x}^{2}}(a\ne 0)\) 】 的图象和性质

以前的知识点总结中有提到，二次函数最简顶点式解析式是：\(\displaystyle y=a{{x}^{2}}(a\ne 0)\) ，在这里我们研究一下它的图象和性质。

其实总的来说二次函数的图象是一条关于某条直线对称的曲线，叫做抛物线，该直线叫做抛物线的对称轴，对称轴与抛物线的交点叫做抛物线的顶点。

对于最简二次函数顶点式解析式\(\displaystyle y=a{{x}^{2}}(a\ne 0)\)来说，我们从两个大的方面来细微的学习一下，两个大的方面下面我们再研究六个小的方面：

一、对于系于a 来说，当a>0时，

1、其图象如下所示：

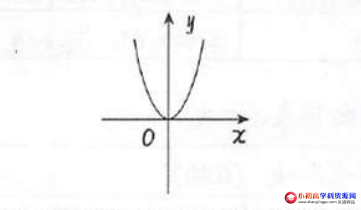
2、图象的开口方向是向上的；

3、顶点坐标为（0，0）；

4、对称轴是y轴（或直线x=0）；

5、增减性：当x<0时，y随x的增大而减少，当x>0是，y随x的增大而增大；

6、最值：当x=0时，y的最小值为0.

二、对于系于a 来说，当a<0时，

1、其图象如下所示：

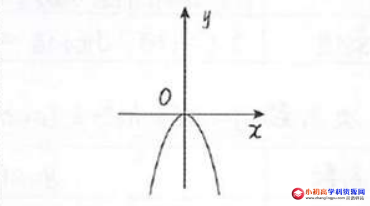
2、图象的开口方向是向下的；

3、顶点坐标为（0，0）；

4、对称轴是y轴（或直线x=0）；

5、增减性：当x<0时，y随x的增大而增大，当x>0是，y随x的增大而减少；

6、最值：当x=0时，y的最大值为0.