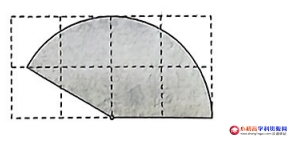
【例题】:如图,格点纸中每个小正方形的边长均为1,以小正方形的顶点为圆心,2为半径做了一个扇形,用该扇形围成一个圆锥的侧面,针对此做法,小明和小亮通过计算得出以下结论:小明说此圆锥的侧面积为\(\displaystyle \frac{5}{6}\pi \);小亮说此圆锥的底面周长为\(\displaystyle \frac{5}{3}\pi \),则下列结论正确的是( )
A.只有小亮对 B.只有小明对 C.两人都对 D.两人都不对
【答案】:A
【解析】:在解这道题时,我们要注意以下两个知识点:
1、圆锥的侧面展开图为一个扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长;
2、圆锥的侧面积:\(\displaystyle {{S}_{侧}}=\frac{1}{2}\times 2\pi rl=\pi rl\)
如图,由题意得:OB=2,OA=1,∠OAB=90°
∵ cos∠AOB=\(\displaystyle \frac{OA}{OB}\)=\(\displaystyle \frac{1}{2}\)
∴ ∠AOB=60°
∴ 该扇形的圆心角为60°+90°=150°
∴ \(\displaystyle {{S}_{扇形}}=\frac{{150\times \pi \times {{2}^{2}}}}{{360}}=\frac{5}{3}\pi \)
\(\displaystyle {{l}_{扇形}}=\frac{{150\times \pi \times 2}}{{180}}=\frac{5}{3}\pi \)
∴ 圆锥的侧面积为\(\displaystyle \frac{5}{3}\pi \),圆锥的底面周长为\(\displaystyle \frac{5}{3}\pi \)
∴ 小明的说法错误,小亮的说法正确


