初中九年级数学知识点总结：二次函数解析式【 y=a乘以x-h的平方 】的图象和性质

初中九年级数学知识点总结：二次函数解析式【\(\displaystyle y=a{{\left( {x-h} \right)}^{2}},\left( {a\ne 0} \right)\) 】的图象和性质

一、二次函数解析式：\(\displaystyle y=a{{\left( {x-h} \right)}^{2}},\left( {a\ne 0} \right)\)

二、图象

1、当 a>0 时，图象为：

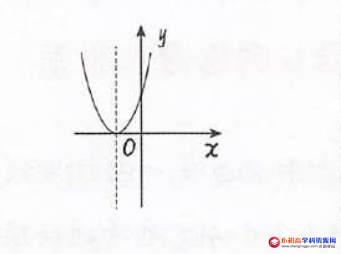
2、当 a<o 时，图象为：

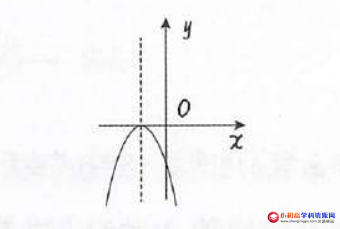
三、开口方向

1、当 a>0 时：开口向上

2、当 a<o 时：开口向下

四、顶点坐标

1、当 a>0 时：顶点坐标为（h,0）

2、当 a<o 时：项点坐标为（h,0）

五、对称轴

1、当 a>0 时：对称轴为直线x=h

2、当 a<o 时：对称轴为直线x=h

六、增减性

1、当 a>0 时：当 x<h 时，y 随 x 的增大而减小；当 x>h 时，y 随 x 的增大而增大。

2、当 a<o 时：当 x<h 时，y 随 x 的增大而增大；当 x>h 时，y 随 x 的增大而减小。

七、最值

1、当 a>0 时，当 x=h 时，y最小值等于0；

2、当 a<o 时，当 x=h 时，y最大值等于0；