张灵谱
阅读模式
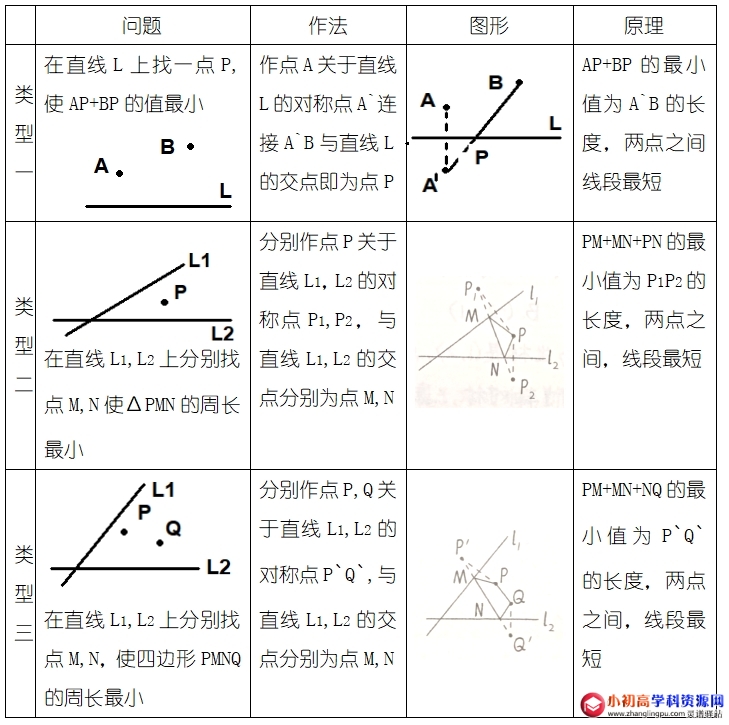
| 问题 | 作法 | 图形 | 原理 | |
| 类型一 | 在直线L上找一点P,使AP+BP的值最小
|
作点A关于直线L的对称点A`连接A`B与直线L的交点即为点P |
|
AP+BP的最小值为A`B的长度，两点之间线段最短 |
| 类型二 |
在直线L1,L2上分别找点M,N使∆PMN的周长最小 |
分别作点P关于直线L1，L2的对称点P1,P2，与直线L1,L2的交点分别为点M,N | PM+MN+PN的最小值为P1P2的长度，两点之间，线段最短 | |
| 类型三 | 在直线L1,L2上分别找点M,N，使四边形PMNQ的周长最小 | 分别作点P,Q关于直线L1,L2的对称点P`Q`,与直线L1,L2的交点分别为点M,N | PM+MN+NQ的最小值为P`Q`的长度，两点之间，线段最短 |
我的微信
微信号已复制
⇐ 加微信，获取海量学习资源！
专注小初高数学教学研究20余年，拥有优质的学科资源，如有需要请联系张老师！