初中数学九年级例题解析：过圆外一点作圆的切线的应用

初中数学九年级例题解析：过圆外一点作圆的切线的应用

【例题】：下面是“过圆外一点作圆的切线”的尺规作图过程，已知：如图1，ΘO和ΘO外一点P，求作：过点P的ΘO的切线。

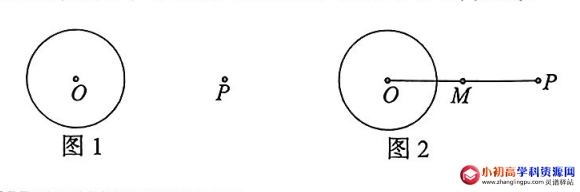
作法：如图2,

1、连接OP，取线段OP的中点M

2、以M为圆心，MP的长为半径作圆，交ΘO于点A,B

3、作直线PA和PB，直线PA,PB即为所求作ΘO的切线

请在图2中补全图形，并完成下面的证明。

证明：连接OA，由作法可知，OP为ΘM的直径

∴  ∠OAP=90°（                  ）（填推理的依据）

∴  OA⊥PA

∵  点A在ΘO上

∴  直线PA是ΘO的切线（                  ）（填推理的依据）

同理，直线PB也是ΘO的切线。

【答案】：直径所对的圆周角为直角，经过半径的外端且垂直于这条半径的直线是圆的切线，补全图形如下：

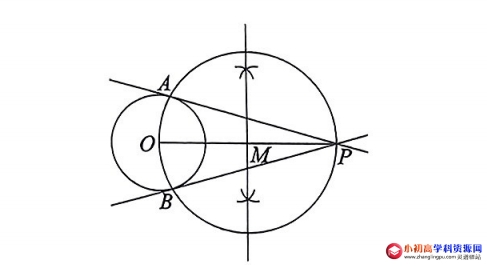
【解析】：过圆外一点作圆的切线是课程标准新增内容，掌握其作法和原理是关键。