初中数学九年级例题解析：锐角三角函数的应用“母子”模型

初中数学九年级例题解析：锐角三角函数的应用“母子”模型

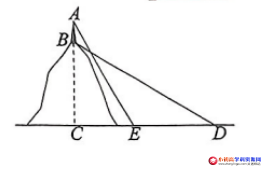
【例题】：(四川眉山  •  中考) 某数学兴趣小组去测量一座小山的高度，如图，在小山顶上有一高度为 20 米的发射塔 AB，在山脚平地上的D处测得塔底 B的仰角为 30°，向小山前进 80米到达点E处，测得塔顶A的仰角为 60°，求小山 BC 的高度。

【答案】：小山BC的高度为\(\displaystyle \left( {10+40\sqrt{3}} \right)\)米

【解析】：首先我们来看下图是常见的2种“母子”模型，通常需要构造两个公共角为直角的三角形。

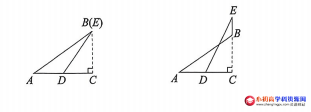
解：设BC为 x 米，则AC=（20+x）米，据题意得：

∠DBC=∠AEC=60° , DE=80米，在直角三角形DBC中

\(\displaystyle \tan {{60}^{\circ }}=\frac{{DC}}{{BC}}=\frac{{DC}}{x}=\sqrt{3}\)，则\(\displaystyle DC=\sqrt{3}x\)米

∴  \(\displaystyle CE=\left( {\sqrt{3}x-80} \right)\)

在直角三角形ACE中，

\(\displaystyle \tan {{60}^{\circ }}=\frac{{AC}}{{CE}}=\frac{{20+x}}{{\sqrt{3}x-80}}=\sqrt{3}\)

解得\(\displaystyle x=10+40\sqrt{3}\)

答：小山BC的高度为\(\displaystyle \left( {10+40\sqrt{3}} \right)\)米